

1. 오늘의 학습 문제
문제
https://www.acmicpc.net/problem/17834
사자와 토끼
| 1 초 | 256 MB | 536 | 289 | 244 | 57.820% |
문제
사자와 토끼는 전국적으로 인기를 끌고 있는 재밌는 보드게임이다. 사자와 토끼를 즐기기 위해서는 2명의 플레이어와 1명의 심판이 필요하다. 보드판은 N개의 수풀과 M개의 오솔길로 이루어져 있다. 오솔길은 서로 다른 두 수풀을 양방향으로 연결하며, 어떤 수풀에서 다른 수풀까지 1개 이상의 오솔길을 통하면 반드시 도달 할 수 있다.
게임은 다음과 같은 순서로 이루어진다.
- 심판이 사자와 토끼의 초기 위치를 각각 어느 수풀로 할지 정한다. 사자와 토끼의 초기 위치는 같을 수 없으며, 사자의 위치는 사자 플레이어에게만, 토끼의 위치는 토끼 플레이어에게만 알려준다.
- 매 턴마다, 사자와 토끼는 현재 위치한 수풀에서 오솔길 1개를 따라 이동해야 한다. 두 플레이어는 자신의 말을 이동할 위치를 심판에게만 말한다. 이동하지 않을 수는 없다.
- 이동한 후, 사자와 토끼가 같은 수풀에 있다면 사자가 토끼를 잡아먹어 게임이 끝난다. 그렇지 않다면, 다시 2로 돌아가 턴을 계속하여 진행한다. 물론 게임이 끝나지 않는 이상, 이동 후에도 두 플레이어는 상대 말의 위치를 알 수 없다. 또한, 사자는 오솔길 위에서는 토끼를 볼 수 없기 때문에, 같은 오솔길을 통해 이동하여도 서로 다른 수풀에 도착했다면 게임이 끝나지 않는다.
이렇게 서로 심리전을 통해 토끼는 사자에게서 도망가고, 사자는 토끼를 찾아내는 게임이다. 그런데 보드의 모양과 사자와 토끼의 초기 위치에 따라서, 어떻게 움직여도 영원히 게임이 끝나지 않는 경우가 있다는 것을 발견했다. 예를 들어, 위의 그림과 같은 보드판에서는 게임이 끝나지 않는 (사자의 초기 위치, 토끼의 초기 위치)의 조합은 다음과 같이 8가지가 존재한다 : (1,2) (1,4) (2,1) (2,3) (3,2) (3,4) (4,1) (4,3). 이런 경우에는, 심지어 두 플레이어가 서로의 위치를 알고 일부러 게임을 끝내려고 해도 끝낼 수 없다!
보드판의 모양이 주어질 때, 어떻게 움직여도 영원히 게임이 끝나지 않는 초기 위치의 경우의 수가 몇 가지가 있을지 구해보자.
입력
첫 번째 줄에 수풀의 수 N(2 ≤ N ≤ 50,000)과 오솔길의 수 M(1 ≤ M ≤ 500,000)이 공백으로 구분되어 주어진다.
두 번째 줄부터 M개의 줄에 걸쳐, u, v(1 ≤ u,v ≤ N, u ≠ v)가 공백으로 구분되어 주어진다. 이는 u번 수풀과 v번 수풀이 오솔길로 연결되어 있음을 의미한다.
출력
첫 번째 줄에 어떻게 움직여도 영원히 게임이 끝나지 않는 초기 위치의 경우의 수를 출력한다.
예제 입력 1 복사
4 4
1 2
2 3
3 4
4 1
예제 출력 1 복사
8
예제 입력 2 복사
2 1
1 2
예제 출력 2 복사
2
예제 입력 3 복사
3 3
1 2
2 3
3 1
예제 출력 3 복사
0
~생각의 흐름~
두 노드의 간격이 홀수면 만날 수 없다는 것을 알았다. 그래서
양방향 그래프를 생성해주어, 가능한 모든 조합에 대해, 두 노드의 모든 가능한 도달 루트를 센다. (DFS) 그때 값 중 짝수가 있으면 조건에 불합.
라고 생각했으나 구현이 잘 되지않아 풀이를 참고했다.
코드
import java.util.*;
import java.io.*;
public class Main {
static List<List<Integer>> graph; // 인접 리스트로 그래프 표현
static int[] color; // 0: 방문하지 않음, 1: 색상 1, -1: 색상 2
static long count1 = 0, count2 = 0; // 두 집합의 크기
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
// 첫 번째 줄에서 수풀의 수 N과 오솔길의 수 M을 입력받음
StringTokenizer st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken());
int m = Integer.parseInt(st.nextToken());
// 그래프 초기화
graph = new ArrayList<>();
for (int i = 0; i < n; i++) {
graph.add(new ArrayList<>());
}
// M개의 오솔길 정보를 입력받아 그래프를 구성
for (int i = 0; i < m; i++) {
st = new StringTokenizer(br.readLine());
int u = Integer.parseInt(st.nextToken()) - 1; // 0-based index로 변환
int v = Integer.parseInt(st.nextToken()) - 1; // 0-based index로 변환
graph.get(u).add(v);
graph.get(v).add(u);
}
// 색상 배열 초기화 (모든 노드를 방문하지 않은 상태로 설정)
color = new int[n];
Arrays.fill(color, 0); // 처음에는 모두 방문하지 않은 상태
boolean isBipartite = true;
// 모든 노드를 방문하면서 이분 그래프인지 확인
for (int i = 0; i < n; i++) {
if (color[i] == 0) { // 해당 노드를 방문하지 않았다면
count1 = 0;
count2 = 0;
if (!dfs(i, 1)) { // DFS를 사용하여 이분 그래프인지 판별
isBipartite = false;
break;
}
}
}
if (isBipartite) {
// 가능한 초기 위치의 조합 수를 계산하여 출력
System.out.println(count1 * count2 * 2);
} else {
// 이분 그래프가 아니면 게임이 끝나지 않는 경우는 없음
System.out.println(0);
}
}
// DFS를 사용하여 그래프가 이분 그래프인지 판별하는 함수
static boolean dfs(int node, int c) {
color[node] = c; // 현재 노드에 색상을 지정
if (c == 1) count1++; // 색상 1에 속하는 노드 개수 증가
else count2++; // 색상 2에 속하는 노드 개수 증가
for (int neighbor : graph.get(node)) {
if (color[neighbor] == 0) { // 이웃 노드를 방문하지 않았다면
if (!dfs(neighbor, -c)) { // 이웃 노드를 반대 색상으로 칠함
return false;
}
} else if (color[neighbor] == color[node]) {
// 이웃 노드가 현재 노드와 같은 색상이라면 이분 그래프가 아님
return false;
}
}
return true;
}
}
2. 오늘의 회고
- 토끼 이미지가 굉장히 귀여웠기에, 오늘은 토끼 이미지를 썸네일로 했다.
- 이분 그래프 개념을 알게 되었다.
이분 그래프(Biparitite Graph)
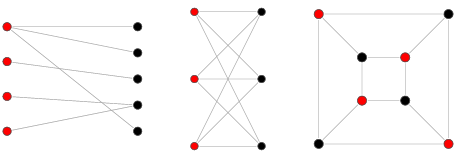
인접한 정점끼리 서로 다른 색으로 칠하여 모든 정점을 두 가지 색으로만 칠할 수 있는 그래프
한 간선은 서로 다른 색의 정점을 가지게 된다.
어떻게 확인하나요?
- BFS/DFS를 이용해 탐색
- BFS: 같은 레벨의 정점은 모두 같은 색임
- 연결 성분의 개수를 구하는 방법과 유사함.
- 모든 정점을 방문하여 간선을 검사→ 시간 복잡도 O(V+E)
💡 KEY: BFS/DFS로 탐색하며 정점을 방문할 때 마다 색을 칠합니다. 자신과 인접한 정점은 다른 색으로 칠하며, 탐색을 진행하면서 인접 정점의 색이 자신과 동일하면 이분 그래프가 아닙니다. 모든 정점을 방문했을 때 전과 같은 경우가 없다면 이분 그래프입니다.
- 아래 이분 그래프 문제를 풀어볼 것!
- https://www.acmicpc.net/problem/1707
#99클럽 #코딩테스트 준비 #개발자 취업 #항해99 #TIL
'공부 > 2024 항해99코딩클럽' 카테고리의 다른 글
| 99클럽 3기 코테 스터디 19일차 TIL /[프로그래머스] 조이스틱 자바 풀이 그리디 문제 (0) | 2024.08.09 |
|---|---|
| 99클럽 3기 코테 스터디 18일차 TIL /[백준] 5547 일루미네이션 BFS 자바 (0) | 2024.08.08 |
| 99클럽 3기 코테 스터디 16일차 TIL /[프로그래머스] N-Queen 자바 (0) | 2024.08.06 |
| 99클럽 3기 코테 스터디 15일차 TIL /[프로그래머스] 소수찾기 자바 (0) | 2024.08.05 |
| 99클럽 3기 코테 스터디 14일차 TIL /[프로그래머스] 징검다리 (0) | 2024.08.04 |




